Learn about the main Boolean algebra identities or laws associated with Boolean logic or digital logic.
Before delving too far into this article, to better understand it, make sure to read the article before this on the basics of Boolean algebra. You might review that article if you find yourself having difficulty following the concepts or notation used here. With that in mind, let's dive into the main Boolean identities associated with Boolean algebra.
Boolean Algebra Laws—What are Boolean Algebra Identities?
Like normal algebra, Boolean algebra has several beneficial identities. An "identity" is merely a relationship that is always true, regardless of the values that any variables involved might take on; similar to laws or properties. Many of these can be analogous to normal multiplication and addition, particularly when the symbols {0,1} are used for {FALSE, TRUE}. However, while this can be useful, some identities are different and that causes confusion for many people. We will be sure to highlight these as we encounter them.
To begin with, Table 1 summarizes these identities, outlines the expressions, and then examines each in detail.
Table 1. Expressions for Boolean identities.
| IDENTITY | EXPRESSION | |
|
Logical Inverse |
$$ \overline{0} = 1; \;\; \overline{1} = 0 $$ |
|
|
Involution |
$$ \overline{\overline{A}} = A $$ |
|
|
|
OR | AND |
|
Dominance |
$$ A + 1 = 1 $$ |
$$ A \cdot 0 = 0 $$ |
|
Identity |
$$ A + 0 = A $$ |
$$ A \cdot 1 = A $$ |
|
Idempotence |
$$ A + A = A $$ |
$$ A \cdot A = A $$ |
|
Complementarity |
$$ A + \overline{A} = 1 $$ |
$$ A \cdot \overline{A} = 0 $$ |
|
Commutativity |
$$ A + B = B + A $$ |
$$ A \cdot B = B \cdot A $$ |
|
Associativity |
$$ (A + B) + C = A + (B + C) $$ |
$$ (A \cdot B) \cdot C = A \cdot (B \cdot C) $$ |
|
Distributivity |
$$ A + (B \cdot C) \; = \; (A + B) \cdot (A + C) $$ |
$$ A \cdot (B + C) = (A \cdot B) + (A \cdot C) $$ |
|
Absorption |
$$ A \cdot (A + B) = A $$ |
$$ A \cdot (A + B) = A $$ |
|
DeMorgan's |
$$ A + B = \overline{\overline{A} \cdot \overline{B}} $$ |
$$ A \cdot B = \overline{ \overline{A} + \overline{B}} $$ |
Each of these identities can be proven by simply creating a fully-enumerated truth table for the expression on the left (of the equality sign, not of the table) and another for the expression on the right. Afterward, the truth table shows that they produce the same result for every possible input combination. For this article's purposes, this approach will be done for each identity.
Despite that being the approach for this article, there is a more elegant way, which is to use previously proven identities to prove subsequent ones. In general, we will not do this primarily because the ordering of the table above is intended to follow a largely intuitive progression and it is not optimized for supporting a chain of Boolean proofs.
It is important to notice that, for each identity involving the OR and/or the AND operator, there is a corresponding identity in which the roles of these two operators are reversed. This is due to the duality of AND and OR.
In all of the expressions in this article, we make no assumption about either the precedence or the associativity of the operators, meaning that we will rely heavily on fully parenthesized expressions. Since we will use the overbar notation for logical negation (the NOT operator), we will use the natural convention that the expression underneath the bar is evaluated and the result of that is then inverted (NOT-ed).
A More Detailed Explanation of Boolean Identities
We will now work our way in order through the table of identities, making observations about each, usually including a "common sense" informal proof. In addition to the Boolean expressions, each identity will also be depicted graphically using standard logic schematic symbols. The symbols for NOT, OR, and AND were introduced in the Boolean Basics article mentioned earlier in this article. In addition to these, we will use the BUF symbol to represent a non-inverting buffer. This gate merely copies its input to its output. Furthermore, while we use {0, 1} to represent {FALSE, TRUE} in the Boolean expressions, we will use {LO, HI} to represent them in the schematic or ladder diagrams.
Figure 1 shows the different symbols for the BUF, NOT, OR, and AND logic gates.

Figure 1.
Notice that the NOT symbol is simply a BUF symbol followed by a bubble. The bubble represents logical inversion and is the actual NOT gate. Anytime you see a bubble attached to a gate pin, you can detach it from the pin and insert a separate NOT gate in its place without affecting the resulting logic.
Each discussion is followed by a formal proof via fully-enumerated truth tables. For most of the identities, these proofs will not contain any surprises. But they are worth including because some of the less-intuitive proofs might make more sense when you can see how the logic progresses through the tables.
Inverse Law
This identity, which is actually two separate identities, is merely the definition of logical negation applied to each of the possible Boolean values.
Below, in Figure 2 you can see an example of LO NOT gates to HI NOT gates and the inverse in Figure 3.

Figure 2.
$$ \overline{0} \; = \; 1 $$

Figure 3.
$$ \overline{1} \; = \; 0 $$
Inverse Law's Boolean Identity Truth Tables
Since this is our first identity, our proof must be based on the fundamental definitions of the signals and the operators (which will be true of several early identities). As the only operation involved here is negation, we simply site the definition of negation and note that these identities are simply the two rows in that definition.
Below, in Tables 2 and 3, you'll find the truth tables for the logical inverse identity.
Table 2.
|
0 |
LHS $$ \overline{0} $$ |
RHS 1 |
|
0 |
1 | 1 |
|
1 |
LHS $$ \overline{1} $$ |
RHS 0 |
|
1 |
0 | 0 |
Involution Law
In mathematics, a function is said to be involute if it is its own inverse. In normal arithmetic (as to Boolean arithmetic), the reciprocal function is involute since the reciprocal of a reciprocal yields the original value, as does multiplying a value twice by -1. In Boolean logic, negation is an involute function because negating a value twice returns the original value (shown in Figure 4). This is analogous to the "double negative" in normal conversation.

Figure 4.
$$ \overline{\overline{A}} \; = A $$ or $$ (A')' \; = \; A $$
Involution Law's Boolean Identity Truth Table
In Table 4, you can see the truth table for the involution law.
Table 4.
|
A |
$$ \overline{A} $$ | $$ \overline{ \left( \overline{A} \right) } \; = \; \overline{\overline{A}} $$ |
LHS $$ \overline{ \overline{A} } $$ |
RHS A |
|
0 |
1 | 0 | 0 | 0 |
|
1 |
0 | 1 | 1 | 1 |
Dominance Law
In normal multiplication, we have the property that anything multiplied by zero yields zero. In a sense, this means that zero has the ability to suppress, mask, or dominate any other value under multiplication. The dominance identity—also known as the "suppression" or "masking" identity"—is similar and merely recognizes that anything that is OR-ed with a TRUE produces a TRUE while anything AND-ed with a FALSE produces a FALSE (see Figures 5 and 6).

Figure 5.
$$ A + 1 = 1 $$

Figure 6.
$$ A \cdot 0 = 0 $$
While the second property looks the same as normal multiplication, the first property is definitely NOT the same as normal addition. This is something to remember until you are proficient with Boolean algebra. This is because it can be easy to fall back on well-entrenched habits and apply rules from normal algebra to Boolean algebra when they simply aren't valid or fail to exploit rules that are.
Dominance Law's Boolean Identity Truth Tables
Below (Tables 5 and 6) you'll see two truth tables for dominance of 1 under OR and dominance of 0 under AND, respectively.
Table 5.
|
A |
1 |
LHS A+1 |
RHS 1 |
|
0 |
1 | 1 | 1 |
|
1 |
1 | 1 | 1 |
Table 6.
| A | 0 |
LHS $$ A \cdot 0 $$ |
RHS 0 |
|
0 |
0 | 0 | 0 |
|
1 |
0 | 0 | 0 |
Note that, technically, the proofs given here only apply to the case when the first input is the free variable and the second input is the dominant value for that operation. We could prove that the identity holds when the inputs are swapped, but once we prove that both OR and AND are commutative, those proofs become trivial and uninteresting.
Identity Law
Just as 0 is the identity element for normal addition and 1 is the identity element for multiplication, so too are 0 (FALSE) and 1 (TRUE) the identity elements for OR and AND respectively. You can see examples of this in Figure 7 and Figure 8.

Figure 7.
$$ A + 0 = A $$

Figure 8.
$$ A \cdot 1 = A $$
This Boolean property, more than anything else, is why the addition symbol is used for logical OR, and the multiplication symbol is used for logical AND. However, it is important to remember that, in Boolean algebra, we are NOT adding or multiplying two values together when we use these operators. Using this terminology can be poor form and generally frowned upon (even though it is heard quite regularly). Having said that, the terms "sum" and "product" are widely used and accepted for the results of logical OR and logical AND, respectively. So while it is poor form to talk about "adding A and B," it is acceptable to talk about "the sum of A and B." This may seem odd and even inconsistent but it is simply the result of a compromise that has evolved between mathematically rigorous terminology and practical common parlance. For instance, it is easier and cleaner to speak of "the sum of products" than it is "the OR of ANDs."
Identity Law's Boolean Identity Truth Tables
The identity for OR comes directly from the definition of OR when the second input is constrained to be 0, while the identity for AND comes directly from its definition when the second input is constrained to be 1. Therefore, our proofs (Table 7 and Table 8) merely consist of the applicable rows from the definitions of these two operators.
Table 7.
|
A |
0 |
LHS A+0 |
RHS A |
|
0 |
0 | 0 | 0 |
|
1 |
0 | 1 | 1 |
Table 8.
| A | 1 |
LHS $$ A \cdot 1 $$ |
RHS A |
|
0 |
1 | 0 | 0 |
|
1 |
1 | 1 | 1 |
Note that, technically, the proofs given here only apply to the case when the first input is the free variable and the second input is the identity value for that operation. We could prove that the identity holds when the inputs are swapped, but once we prove that both OR and AND are commutative, those proofs become trivial and uninteresting.
Idempotent Law
The term "idempotent" describes an operation that can be carried out any number of times and the effect is the same as if it had only been carried out once. If we either AND a Boolean variable with itself or OR it with itself, we get the same result as the original variable. This means that both AND and OR are idempotent. This property can be expressed in Figure 9 and Figure 10.

Figure 9.
$$ A + A = A $$

Figure 10.
$$ A \cdot A = A $$
Notice that this is very different than normal arithmetic.
Idempotent Law's Boolean Identity Truth Tables
The proof (Tables 9 and 10) of idempotence for both OR and AND follows from examining the definition of each operation under the constraint that both inputs have the same value.
Table 9.
|
A |
A |
LHS A+A |
RHS A |
|
0 |
0 | 0 | 0 |
|
1 |
1 | 1 | 1 |
Table 10.
| A | A |
LHS $$ A \cdot A $$ |
RHS A |
|
0 |
0 | 0 | 0 |
|
1 |
1 | 1 | 1 |
Complement Law
A 'complement' (as opposed to a 'compliment') is the opposite of something. In fact, another name for the logical inverse is the complement. When we OR or AND a Boolean value with its complement we end up with the same result regardless of the variable's value. In the case of AND, since we know that either the variable or its complement is FALSE, the logical AND of a variable with its complement will always yield FALSE since the one that is FALSE will dominate. Similarly, since we know one of them is TRUE, the logical OR of a variable with its complement will always yield TRUE because the one that is TRUE will dominate.
You can see this below in Figure 11 and Figure 12.

Figure 11.
$$ A + \overline{A} = 1 $$

Figure 12.
$$ A \cdot \overline{A} = 0 $$
Since this identity only applies when the two inputs are different, our proof merely examines the rows of our defining functions where that is the case. This is a surprisingly powerful identity that often plays a part in reducing or simplifying Boolean expressions.
Complement Law's Boolean Identity Truth Tables
To have the property of complementarity, all that is required of a Boolean binary operator is that it be symmetric, meaning that the two rows in its defining truth table (Table 11 and Table 12) with dissimilar inputs produce the same result.
Table 11.
|
A |
$$ \overline{A} $$ |
LHS $$ A + \overline{A} $$ |
RHS 1 |
|
0 |
1 | 1 | 1 |
|
1 |
0 | 1 | 1 |
Table 12.
| A | $$ \overline{A} $$ |
LHS $$ A \cdot \overline{A} $$ |
RHS 0 |
|
0 |
1 | 0 | 0 |
|
1 |
0 | 0 | 0 |
Note that, technically, the proofs given here only apply to the case when the first input is the uncomplemented free variable and the second input is its complement. We could prove that the identity holds when the inputs are swapped, but once we prove that both OR and AND are commutative, those proofs become trivial and uninteresting.
Commutative Law
As in normal arithmetic, the order of the operands for both OR and AND do not matter making them both commutative. Examples can be seen in Figures 13 and 14.

Figure 13.
$$ A + B = B + A $$

Figure 14.
$$ A \cdot B = B \cdot A $$
This is also described by saying that AND and OR are 'symmetric' functions.
Commutative Law's Boolean Identity Truth Tables
Like complementarity, all that is required for a binary Boolean operator to be commutative is for the two rows in the defining truth table (Tables 13 and 14) to have dissimilar inputs to produce the same output. The corollary to this is that any binary Boolean operator that is commutative is also complementary and vice versa.
Table 13.
|
A |
B |
LHS A + B |
RHS B + A |
|
0 |
0 | 0 | 0 |
|
0 |
1 | 1 | 1 |
|
1 |
0 | 1 | 1 |
|
1 |
1 | 1 | 1 |
Table 14.
| A | B |
LHS $$ A \cdot B $$ |
RHS $$ A \cdot B $$ |
|
0 |
0 | 0 | 0 |
|
0 |
1 | 0 | 0 |
|
1 |
0 | 0 | 0 |
|
1 |
1 | 1 | 1 |
Associative Law
Again, as in normal arithmetic with addition and multiplication, the order in which we apply operations when two or more of the same operator are involved does not matter (shown in Figures 15 and 16).
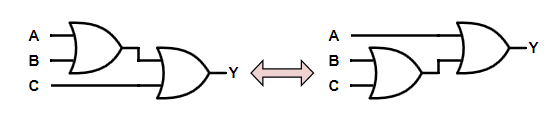
Figure 15.
$$ (A + B) + C = A + (B + C) $$

Figure 16.
$$ (A \cdot B) \cdot C = A \cdot (B \cdot C) $$
The associativity of OR and AND is not at all obvious. It is tempting to assume that because OR and AND are commutative that they must be associative also. This is not the case, however, and some commutative Boolean operators are not associative. Examples include NAND and NOR.
Associative Law's Boolean Identity Truth Tables
Below you'll find the truth tables of associativity under OR (Table 15) and associativity under AND (Table 16).
Table 15.
| A |
B |
C | (A + B) | (B + C) |
LHS (A + B) + C |
RHS A + (B + C) |
| 0 |
0 |
0 | 0 | 0 | 0 | 0 |
| 0 |
0 |
1 | 0 | 1 | 1 | 1 |
| 0 |
1 |
0 | 1 | 1 | 1 | 1 |
| 0 |
1 |
1 | 1 | 1 | 1 | 1 |
|
1 |
0 | 0 | 1 | 0 | 1 | 1 |
|
1 |
0 | 1 | 1 | 1 | 1 | 1 |
|
1 |
1 | 0 | 1 | 1 | 1 | 1 |
|
1 |
1 | 1 | 1 | 1 | 1 | 1 |
Table 16.
| A |
B |
C | $$ (A \cdot B) $$ | $$ (B \cdot C) $$ |
LHS $$ (A \cdot B) \cdot C $$ |
RHS $$ A \cdot (B \cdot C) $$ |
| 0 |
0 |
0 | 0 | 0 | 0 | 0 |
| 0 |
0 |
1 | 0 | 0 | 0 | 0 |
| 0 |
1 |
0 | 0 | 0 | 0 | 0 |
| 0 |
1 |
1 | 0 | 1 | 0 | 0 |
|
1 |
0 | 0 | 0 | 0 | 0 | 0 |
|
1 |
0 | 1 | 0 | 0 | 0 | 0 |
|
1 |
1 | 0 | 1 | 0 | 0 | 0 |
|
1 |
1 | 1 | 1 | 1 | 1 | 1 |
Distributive Law
In normal arithmetic, we often use the property that multiplication distributes over addition and know that addition does not distribute over multiplication. However, in Boolean algebra, either operator distributes over the other. Figures 17 and 18 show examples of this.

Figure 17.
$$ A + (B \cdot C) = (A + B) \cdot (A + C) $$

Figure 18.
$$ A \cdot (B + C) = (A \cdot B) + (A \cdot C) $$
That OR distributes over AND goes against our engrained understanding of the rules of arithmetic and therefore seems very unnatural. Many people are unaware that it is true or actively believe that it is not true. This is almost entirely an unintended consequence of using the plus-sign and multiplication-sign from normal arithmetic and failing to remember that logical operators and arithmetic operators are simply not the same things. Also that they have absolutely no relation to each other regardless of whether we use the symbols to represent them.
Both of these properties can be extremely useful. It's not surprising that many people can make their work much more difficult because they aren't adept at recognizing where applying the distributivity of OR over AND would greatly streamline things.
Distributive Law's Boolean Identity Truth Tables
Table 17 shows the distributivity of AND over OR's truth table, while Table 18 shows the distributivity of OR over AND.
| A |
B |
C | (B + C) | $$ (A \cdot B) $$ | $$ (A \cdot C) $$ |
LHS $$ A \cdot (B + C) $$ |
RHS $$ (A \cdot B) + (A \cdot C) $$ |
| 0 |
0 |
0 | 0 | 0 | 0 | 0 | 0 |
| 0 |
0 |
1 | 1 | 0 | 0 | 0 | 0 |
| 0 |
1 |
0 | 1 | 0 | 0 | 0 | 0 |
| 0 |
1 |
1 | 1 | 0 | 0 | 0 | 0 |
|
1 |
0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
1 |
0 | 1 | 1 | 0 | 1 | 1 | 1 |
|
1 |
1 | 0 | 1 | 1 | 0 | 1 | 1 |
|
1 |
1 | 1 | 1 | 1 | 1 | 1 | 1 |
| A |
B |
C | $$ (B \cdot C) $$ | $$ (A + B) $$ | $$ (A + C) $$ |
LHS $$ A + (B \cdot C) $$ |
RHS $$ (A + B) \cdot (A + C) $$ |
| 0 |
0 |
0 | 0 | 0 | 0 | 0 | 0 |
| 0 |
0 |
1 | 0 | 0 | 1 | 0 | 0 |
| 0 |
1 |
0 | 0 | 1 | 0 | 0 | 0 |
| 0 |
1 |
1 | 1 | 1 | 1 | 1 | 1 |
|
1 |
0 | 0 | 0 | 1 | 1 | 1 | 1 |
|
1 |
0 | 1 | 0 | 1 | 1 | 1 | 1 |
|
1 |
1 | 0 | 0 | 1 | 1 | 1 | 1 |
|
1 |
1 | 1 | 1 | 1 | 1 | 1 | 1 |
Absorption Law
One of the more useful Boolean identities is absorption because it allows users to remove unneeded variables. However, in addition, it also allows us to introduce variables that then frequently allow us to make even greater simplifications (shown in Figures 19 and 20).

Figure 19.
$$ A + (A \cdot B) = A $$

Figure 20.
$$ A \cdot (A + B) = A $$
Informally, these identities make sense by considering the possible options. In the first case, if A is FALSE, then the entire expression is FALSE, while if A is TRUE then (A + B) is TRUE regardless of the value of B and the expression overall is TRUE. Thus, in either case, the overall expression is equal to the value of A alone.
In the second case, this is even more obvious. If A is TRUE then the overall expression is TRUE, while if A is FALSE the second term is FALSE regardless of the value of B and the overall expression is FALSE. Again, the overall expression is equal to the value of A alone.
These two identities tend to be ones that are difficult for people to recall. Therefore it is useful to see an algebraic proof because the manipulations involved are often easier for people to see and apply than the identities themselves.
In the first identity, we can either "factor out" the A using the distributive property of AND over OR or we can just distribute the OR over the AND. Let's use the first approach as this is the one that is usually easier to see in practice.
The second identity is actually more intuitive as seen by first distributing the A using the distributive property of AND over OR and then, after applying idempotence, factoring it back out.
Absorption Law's Boolean Identity Truth Tables
Below, Table 19 shows the truth table for the absorption under OR, and Table 20 shows the absorption under AND.
|
A |
B | $$ (A + B) $$ |
LHS $$ A \cdot (A + B) $$ |
RHS A |
|
0 |
0 | 0 | 0 | 0 |
|
0 |
1 | 1 | 1 | 0 |
|
1 |
0 | 1 | 1 | 1 |
|
1 |
1 | 1 | 1 | 1 |
| A | B | $$ (A \cdot B) $$ |
LHS $$ A + (A \cdot B) $$ |
RHS A |
|
0 |
0 | 0 | 0 | 0 |
|
0 |
1 | 0 | 0 | 0 |
|
1 |
0 | 0 | 1 | 1 |
|
1 |
1 | 1 | 1 | 1 |
DeMorgan's Theorems of Boolean Logic
DeMorgan's identities, better known as DeMorgan's Theorems, can be extremely powerful and heavily used properties of Boolean logic. In essence, they say that an OR gate can be swapped with an AND gate (and vice-versa) without changing the logic function being implemented provided that ALL of the inputs and outputs to the gate are inverted as well (Figure 21 and Figure 22).

Figure 21.
$$ A + B = \overline{ \overline{A} \cdot \overline{B} } $$

Figure 22.
$$ A \cdot B = \overline{ \overline{A} + \overline{B} } $$
Recalling that a bubble on either an input or an output of a gate represents logical inversion, DeMorgan's Theorems can be captured compactly as follows in Figure 23.

Figure 23.
DeMorgan's Theorem Truth Tables
Below in Tables 21 and 22, you'll find example truth tables for DeMorgan's Theorem.
|
A |
B | A + B | $$ \overline{A} $$ |
|
|
LHS $$ A + B $$ |
RHS
|
|
0 |
0 | 0 | 1 | 1 | 1 | 0 | 0 |
|
0 |
1 | 1 | 1 | 0 | 0 | 1 | 1 |
|
1 |
0 | 1 | 0 | 1 | 0 | 1 | 1 |
|
1 |
1 | 1 | 0 | 0 | 0 | 1 | 1 |
|
A |
B | $$ A \cdot B $$ | $$ \overline{A} $$ |
|
|
LHS $$ A \cdot B $$ |
RHS
|
|
0 |
0 | 0 | 1 | 1 | 1 | 0 | 0 |
|
0 |
1 | 0 | 1 | 0 | 1 | 0 | 0 |
|
1 |
0 | 0 | 0 | 1 | 1 | 0 | 0 |
|
1 |
1 | 1 | 0 | 0 | 0 | 1 | 1 |
Continuing Your Boolean Logic Education
Armed with the identities presented here, you are in a position to manipulate Boolean logic expressions and logic diagrams. However, these identities are merely the most fundamental of tools available to you as a logic designer. To become truly proficient at the art, you must also learn some of the many powerful analysis and design techniques that are based upon these fundamentals.








Excellent article!